精读《手写 SQL 编译器 - 语法分析》
1 引言
接着上周的文法介绍,本周介绍的是语法分析。
以解析顺序为角度,语法分析分为两种,自顶而下与自底而上。
自顶而下一般采用递归下降方式处理,称为 LL(k),第一个 L 是指从左到右分析,第二个 L 指从左开始推导,k 是指超前查看的数量,如果实现了回溯功能,k 就是无限大的,所以带有回溯功能的 LL(k) 几乎是最强大的。LL 系列一般分为 LL(0)、LL(1)、LL(k)、LL(∞)。
自底而上一般采用移进(shift)规约(reduce)方式处理,称为 LR,第一个 L 也是从左到右分析,第二个 R 指从右开始推导,而规约时可能产生冲突,所以通过超前查看一个符号解决冲突,就有了 SLR,后面还有功能更强的 LALR(1) LR(1) LR(k)。
通过这张图可以看到 LL 家族与 LR 家族的能力范围:
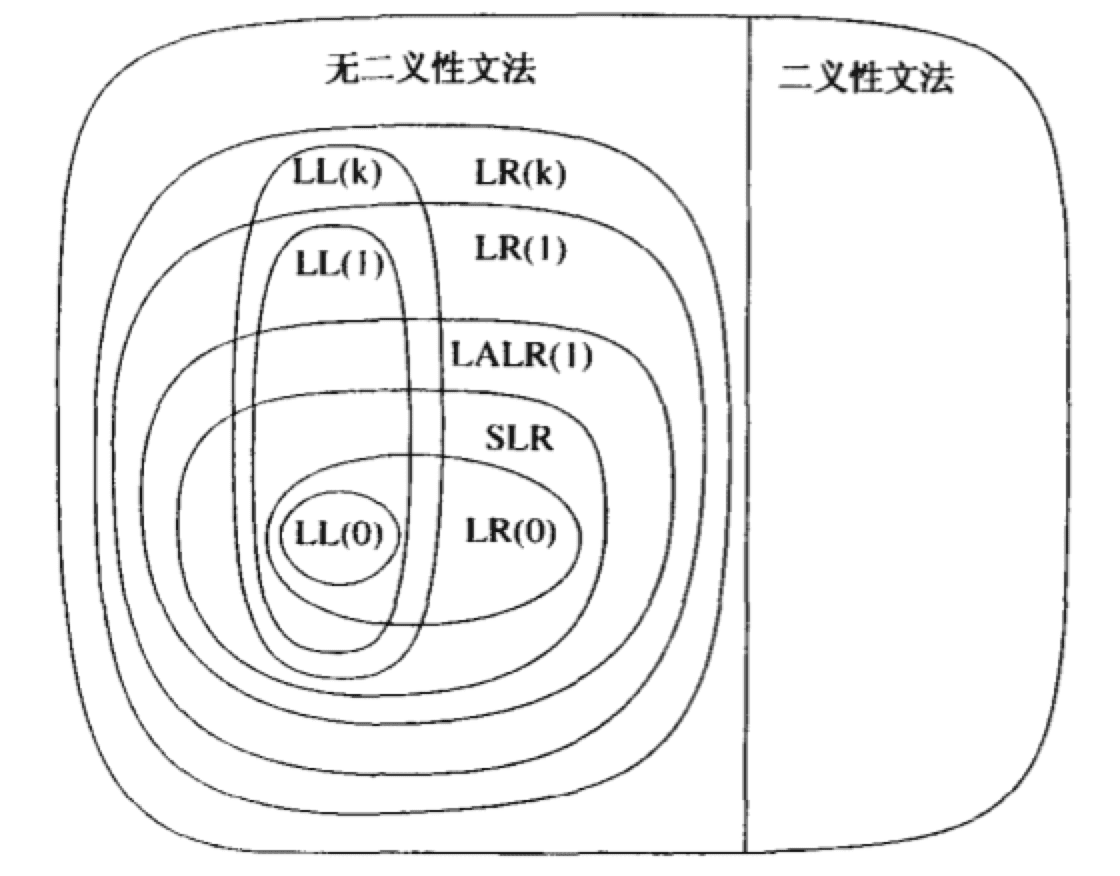
如图所示,无论 LL 还是 LR 都解决不了二义性文法,还好所有计算机语言都属于无二义性文法。
值得一提的是,如果实现了回溯功能的 LL(k) -> LL(∞),那么能力就可以与 LR(k) 所比肩,而 LL 系列手写起来更易读,所以笔者采用了 LL 方式书写,今天介绍如何手写无回溯功能的 LL。
另外也有一些根据文法自动生成 parser 的库,比如兼容多语言的 antlr4 或者对 js 支持比较友好的 pegjs。
2 精读
递归下降可以理解为走多出口的迷宫:
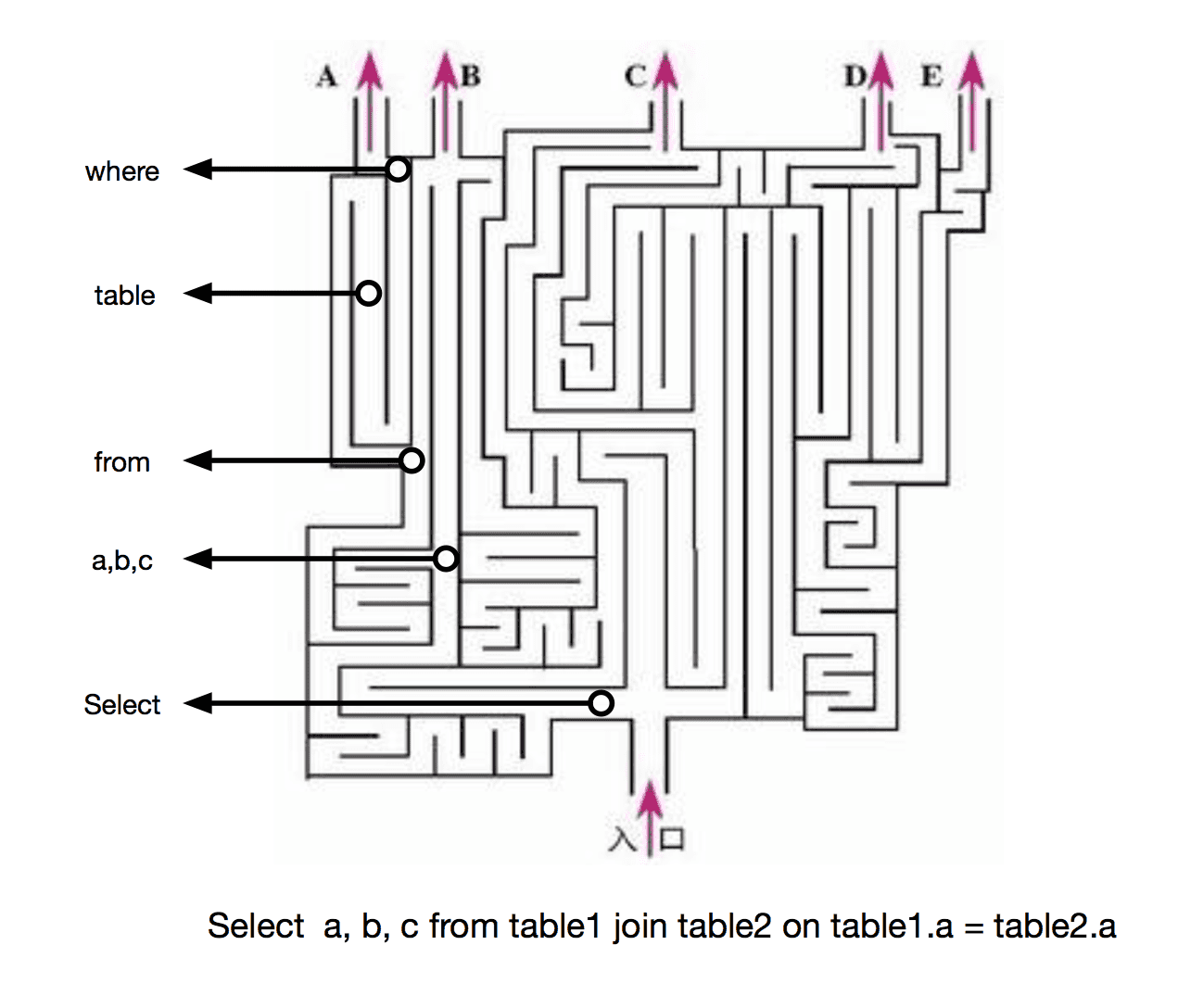
我们先根据 SQL 语法构造一个迷宫,进迷宫的不是探险家,而是 SQL 语句,这个 SQL 语句会拿上一堆令牌(切分好的 Tokens,详情见 精读:词法分析),迷宫每前进一步都会要求按顺序给出令牌(交上去就没收),如果走到出口令牌刚好交完,就成功走出了迷宫;如果出迷宫时手上还有令牌,会被迷宫工作人员带走。这个迷宫会有一些分叉,在分岔路上会要求你亮出几个令牌中任意一个即可通过(LL1),有的迷宫允许你失败了存档,只要没有走出迷宫,都可以读档重来(LLk),理论上可以构造一个最宽容的迷宫,只要还没走出迷宫,可以在分叉处任意读档(LL∞),这个留到下一篇文章介绍。
词法分析
首先对 SQL 进行词法分析,拿到 Tokens 列表,这些就是探险家 SQL 带上的令牌。
根据上次讲的内容,我们对 select a from b 进行词法分析,可以拿到四个 Token(忽略空格与注释)。
Match 函数
递归下降最重要的就是 Match 函数,它就是迷宫中索取令牌的关卡。每个 Match 函数只要匹配上当前 Token 便将 Token index 下移一位,如果没有匹配上,则不消耗 Token:
function match(word: string) {
const currentToken = tokens[tokenIndex] // 拿到当前所在的 Token
if (currentToken.value === word) {
// 如果 Token 匹配上了,则下移一位,同时返回 true
tokenIndex++
return true
}
// 没有匹配上,不消耗 Token,但是返回 false
return false
}
Match 函数就是精简版的 if else,试想下面一段代码:
if (token[tokenIndex].value === 'select') {
tokenIndex++
} else {
return false
}
if (token[tokenIndex].value === 'a') {
tokenIndex++
} else {
return false
}
通过不断对比与移动 Token 进行判断,等价于下面的 Match 实现:
match('select') && match('a')
这样写出来的语法分析代码可读性会更强,我们能专注精神在对文法的解读上,而忽略其他环境因素。
顺便一提,下篇文章笔者会带来更精简的描述方法:
chain('select', 'a')
让函数式语法更接近文法形式。
最后这种语法不但描述更为精简,而且拥有 LL(∞) 的查找能力,拥有几乎最强大的语法分析能力。
语法分析主体函数
既然关卡(Match)已经有了,下面开始构造主函数了,可以开始画迷宫了。
举个最简单的例子,我们想匹配 select a from b,只需要这么构造主函数:
let tokenIndex = 0
function match() { /* .. */ }
const root = () => match("select") && match("a") && match("from") && match("b")
tokens = lexer("select a from b")
if (root() && tokenIndex === tokens.length) {
// sql 解析成功
}
为了简化流程,我们把 tokens、tokenIndex 作为全局变量。首先通过 lexer 拿到 select a from b 语句的 Tokens:['select', ' ', 'a', ' ', 'from', ' ', 'b'],注意在语法解析过程中,注释和空格可以消除,这样可以省去对空格和注释的判断,大大简化代码量。所以最终拿到的 Tokens 是 ['select', 'a', 'from', 'b']。
很显然这样与我们构造的 Match 队列相吻合,所以这段语句顺利的走出了迷宫,而且走出迷宫时,Token 正好被消费完(tokenIndex === tokens.length)。
这样就完成了最简单的语法分析,一共十几行代码。
函数调用
函数调用是 JS 最最基础的知识,但用在语法解析里可就不那么一样了。
考虑上面最简单的语句 select a from b,显然无法胜任真正的 SQL 环境,比如 select [位置] from b 这个位置可以放置任意用逗号相连的字符串,我们如果将这种 SQL 展开描述,将非常复杂,难以阅读。恰好函数调用可以帮我们完美解决这个问题,我们将这个位置抽象为 selectList 函数,所以主语句改造如下:
const root = () =>
match("select") && selectList() && match("from") && match("b")
这下能否解析 select a, b, c from table 就看 selectList 这个函数了:
const selectList =
match("a") && match(",") && match("b") && match(",") && match("c")
显然这样做不具备通用性,因为我们将参数名与数量固定了。考虑到上期精读学到的文法,我们可以这样描述 selectList:
selectList ::= word (',' selectList)?
word ::= [a-zA-Z]
故意绕过了左递归,采用右递归的写法,因而避开了语法分析的核心难点。
? 号是可选的意思,与正则的 ? 类似。
这是一个右递归文法,不难看出,这个文法可以如此展开:
selectList => word (',' selectList)? => a (',' selectList)? => a, word (',' selectList)? => a, b, word (',' selectList)? => a, b, word => a, b, c
我们一下遇到了两个问题:
- 补充 word 函数。
- 如何描述可选参数。
同理,利用函数调用,我们假定拥有了可选函数 optional,与函数 word,这样可以先把 selectList 函数描述出来:
const selectList = () => word() && optional(match(",") && selectList())
这样就通过可选函数 optional 描述了文法符号 ?。
我们来看 word 函数如何实现。需要简单改造下 match 使其支持正则,那么 word 函数可以这样描述:
const word = () => match(/[a-zA-Z]*/)
而 optional 不是普通的 match 函数,从调用方式就能看出来,我们提到下一节详细介绍。
注意 selectList 函数的尾部,通过右递归的方式调用 selectList,因此可以解析任意长度以 , 分割的字段列表。
Antlr4 支持左递归,因此文法可以写成 selectList ::= selectList (, word)? | word,用在我们这个简化的代码中会导致堆栈溢出。
在介绍 optional 函数之前,我们先引出分支函数,因为可选函数是分支函数的一种特殊形式(猜猜为什么?)。
分支函数
我们先看看函数 word,其实没有考虑到函数作为字段的情况,比如 select a, SUM(b) from table。所以我们需要升级下 selectList 的描述:
const selectList = () => field() && optional(match(",") && selectList())
const field = () => word()
这时注意 field 作为一个字段,也可能是文本或函数,我们假设拥有函数处理函数 functional,那么用文法描述 field 就是:
field ::= text | functional
| 表示分支,我们用 tree 函数表示分支函数,那么可以如此改写 field:
const field = () => tree(word(), functional())
那么改如何表示 tree 呢?按照分支函数的特性,tree 的职责是超前查看,也就是超前查看 word 是否符合当前 Token 的特征,如何符合,则此分支可以走通,如果不符合,同理继续尝试 functional。
若存在 A、B 分支,由于是函数式调用,若 A 分支为真,则函数堆栈退出到上层,若后续尝试失败,则无法再回到分支 B 继续尝试,因为函数栈已经退出了。这就是本文开头提到的 回溯 机制,对应迷宫的 存档、读档 机制。要实现回溯机制,要模拟函数执行机制,拿到函数调用的控制权,这个下篇文章再详细介绍。
根据这个特性,我们可以写出 tree 函数:
function tree(...args: any[]) {
return args.some(arg => arg())
}
按照顺序执行 tree 的入参,如果有一个函数执行为真,则跳出函数,如果所有函数都返回 false,则这个分支结果为 false。
考虑到每个分支都会消耗 Token,所以我们需要在执行分支时,先把当前 TokenIndex 保存下来,如果执行成功则消耗,执行失败则还原 Token 位置:
function tree(...args: any[]) {
const startTokenIndex = tokenIndex
return args.some(arg => {
const result = arg()
if (!result) {
tokenIndex = startTokenIndex // 执行失败则还原 TokenIndex
}
return result
});
}
可选函数
可选函数就是分支函数的一个特例,可以描述为:
func? => func | ε
ε 表示空,也就是这个产生式解析到这里永远可以解析成功,而且不消耗 Token。借助分支函数 tree 执行失败后还原 TokenIndex 的特性,我们先尝试执行它,执行失败的话,下一个 ε 函数一定返回 true,而且会重置 TokenIndex 且不消耗 Token,这与可选的含义是等价的。
所以可以这样描述 optional 函数:
const optional = fn => tree(fn, () => true)
基本的运算连接
上面通过对 SQL 语句的实践,发现了 match 匹配单个单词、 && 连接、tree 分支、ε 空字符串的产生式这四种基本用法,这是符合下面四个基本文法组合思想的:
G ::= ε
空字符串产生式,对应 () => true,不消耗 Token,总是返回 true。
G ::= t
单词匹配,对应 match(t)。
G ::= x y
连接运算,对应 match(x) && match(y)。
G ::= x
G ::= y
并运算,对应 tree(x, y)。
有了这四种基本用法,几乎可以描述所有 SQL 语法。
比如简单描述一下 select 语法:
const root = () => match("select") && select() && match("from") && table()
const selectList = () => field() && optional(match(",") && selectList())
const field = () => tree(word, functional)
const word = () => match(/[a-zA-Z]+/)
3 总结
递归下降的 SQL 语法解析就是一个走迷宫的过程,将 Token 从左到右逐个匹配,最终能找到一条路线完全贴合 Token,则 SQL 解析圆满结束,这个迷宫采用空字符串产生式、单词匹配、连接运算、并运算这四个基本文法组合就足以构成。
掌握了这四大法宝,基本的 SQL 解析已经难不倒你了,下一步需要做这些优化:
- 回溯功能,实现它才可能实现 LL(∞) 的匹配能力。
- 左递归自动消除,因为通过文法转换,会改变文法的结合律与语义,最好能实现左递归自动消除(左递归在上一篇精读 文法 有说明)。
- 生成语法树,仅匹配语句的正确性是不够的,我们还要根据语义生成语法树。
- 错误检查,在错误的地方给出建议,甚至对某些错误做自动修复,这个在左 SQL 智能提示时需要用到。
- 错误恢复。
下篇文章会介绍如何实现回溯,让递归下降达到 LL(∞) 的效果。
从本文不难看出,通过函数调用方式我们无法做到 迷宫存档和读档机制,也就是遇到岔路 A B 时,如果 A 成功了,函数调用栈就会退出,而后面迷宫探索失败的话,我们无法回到岔路 B 继续探索。而 回溯功能就赋予了这个探险者返回岔路 B 的能力。
为了实现这个功能,几乎要完全推翻这篇文章的代码组织结构,不过别担心,这四个基本组合思想还会保留。
下篇文章也会放出一个真正能运行的,实现了 LL(∞) 的代码库,函数描述更精简,功能(比这篇文章的方法)更强大,敬请期待。
4 更多讨论
如果你想参与讨论,请点击这里,每周都有新的主题,周末或周一发布。
发表评论 (审核通过后显示评论):